Diffusion 模型
〇、写在前边
DDPM(Denoising Diffusion Probabilistic Models)
一、目录
- 扩散模型的基础
- Stable Diffusion
- 背后的数学原理
二、内容
1. 扩散模型的基础
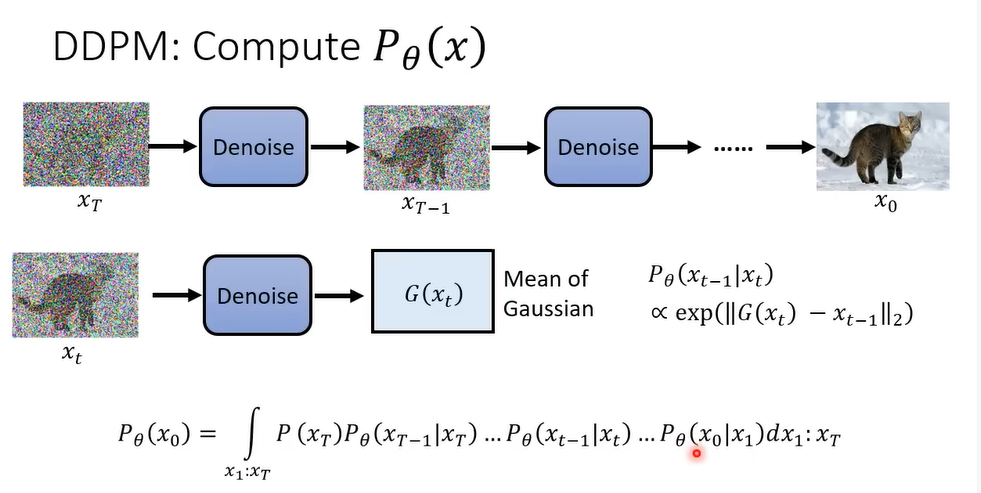
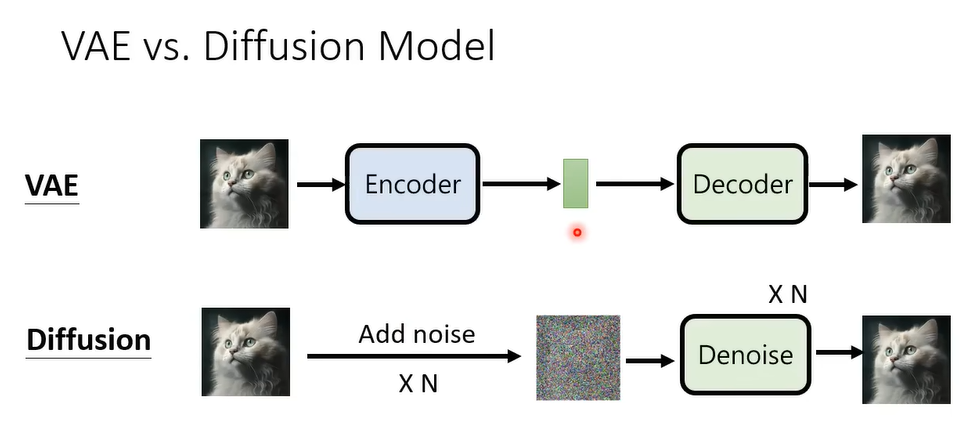
反向过程:采样Sample -> Denoise去噪 -> … -> 图片
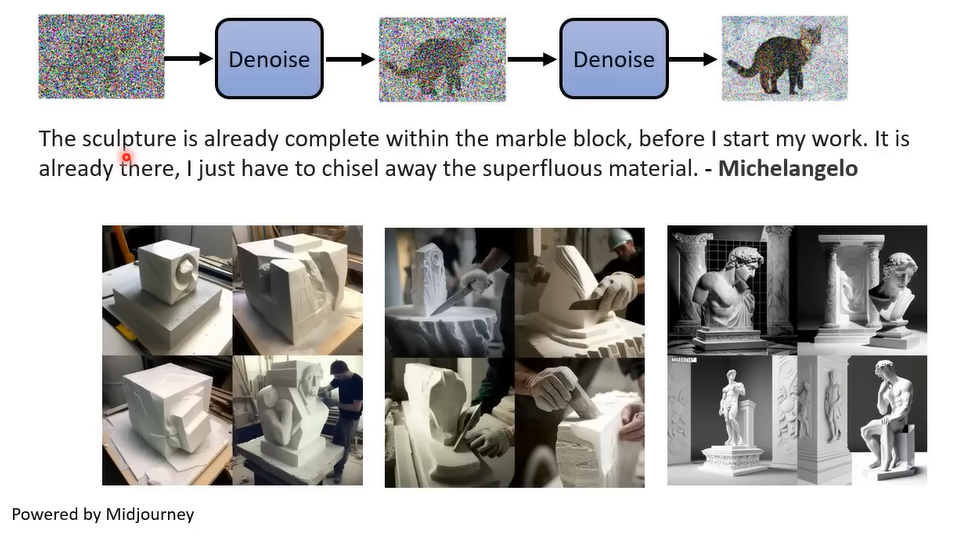
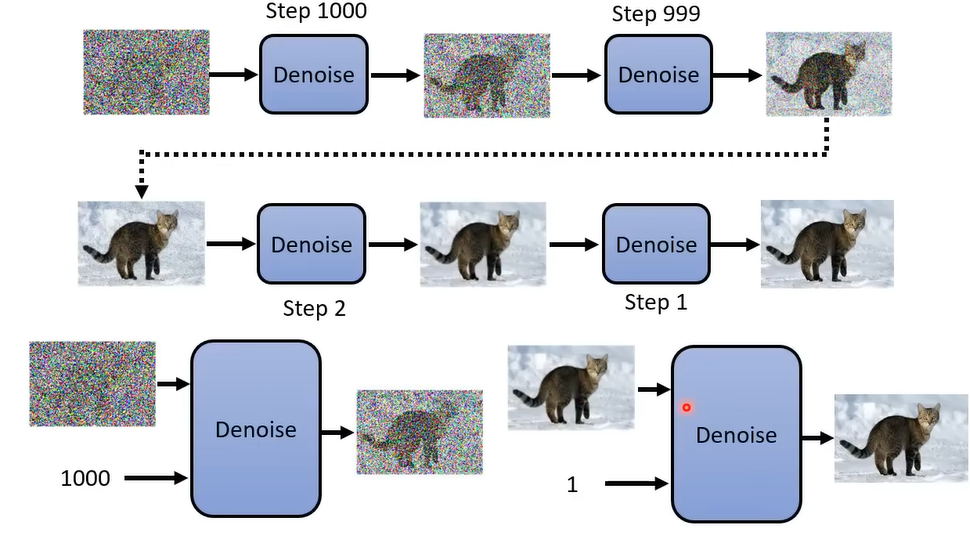
为每一步标号,代表噪声的大小,同时输入到Denoise的模型里面。
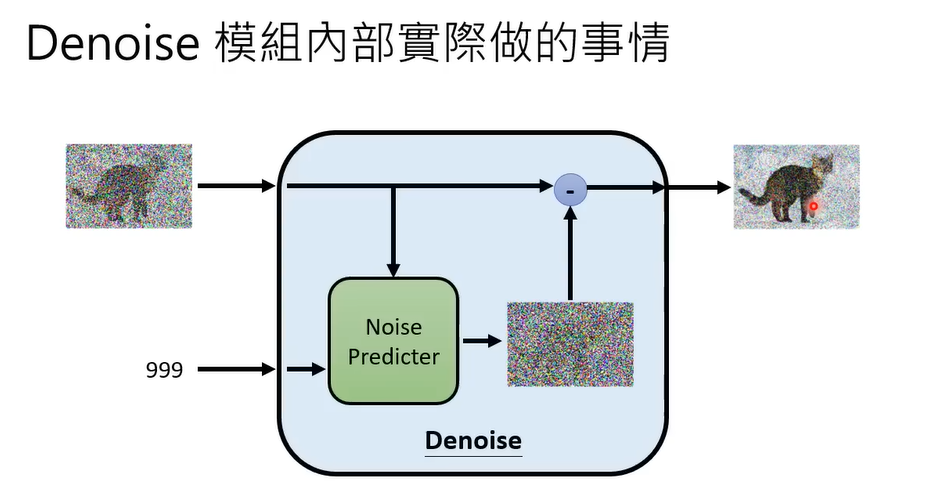
Denoise内部预测噪声长什么样,然后进行去噪。
如何训练Noise Predicter?需要有真实的噪声才能学习出来噪声。而这个噪声就是人为创造的。这个过程叫Forword process。
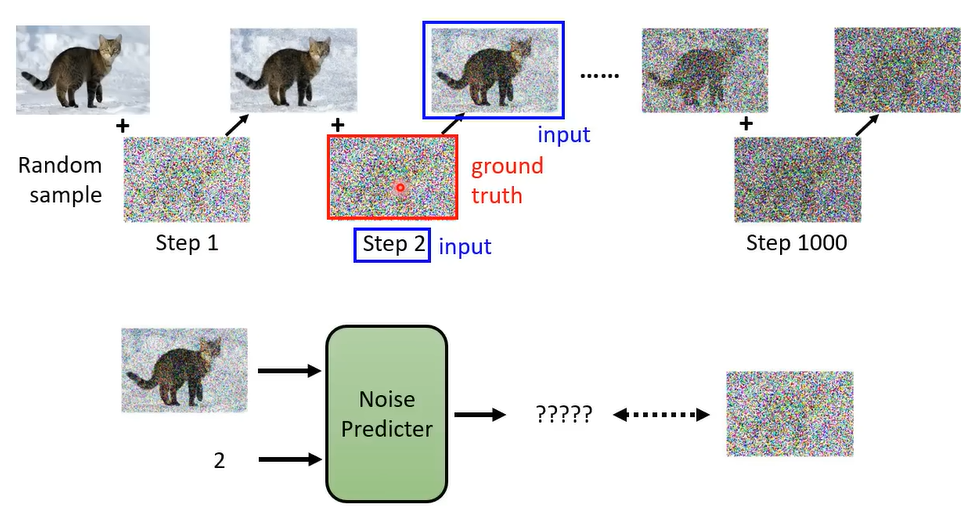
而常见的字生图就是参考了文字+图像的成对资料。https://laion.ai/blog/laion-5b/
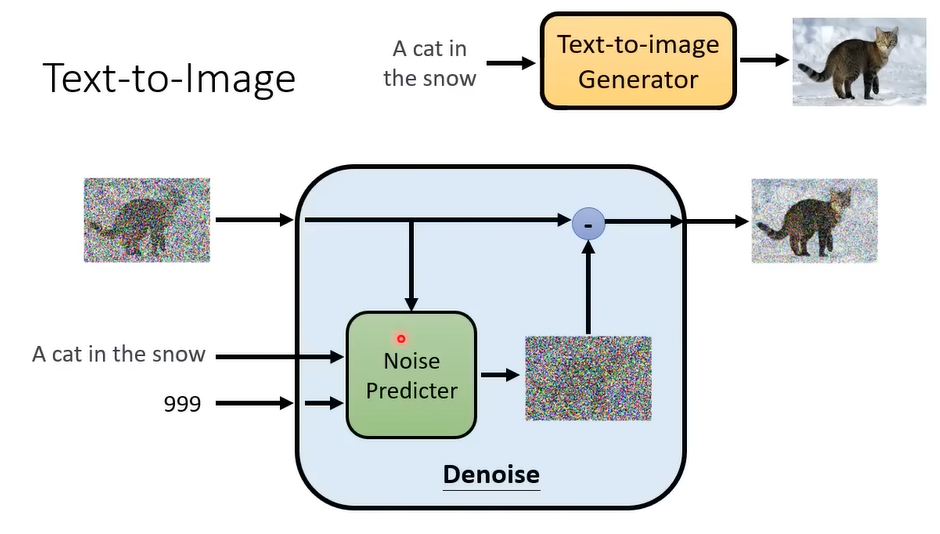
向前加噪也是加上文字即可。
原论文中的算法描述:


2. Stable Diffusion
https://arxiv.org/abs/2112.10752
Encoder + Diffusion + Decoder
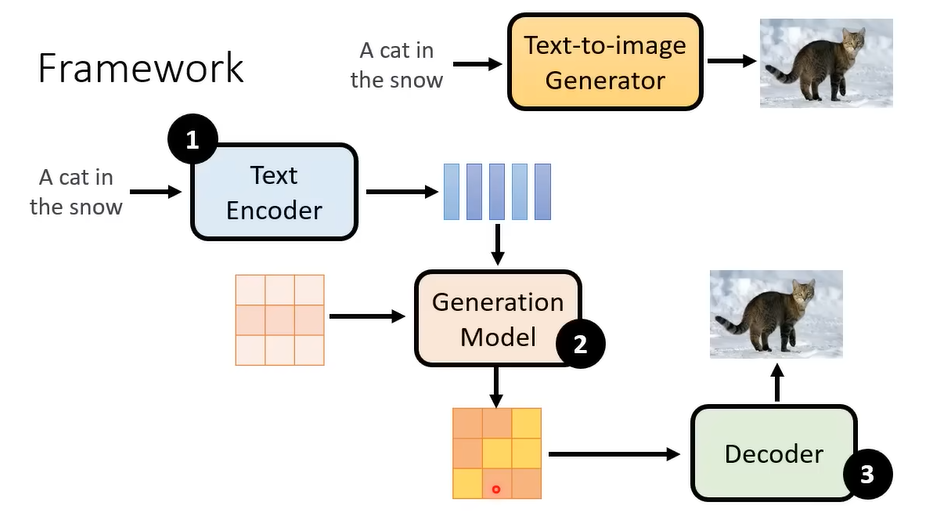
训练Encoder - 评估标准:
FID:图形经过表征之后的分布接近程度。假设表征分布是高斯分布,计算一个“距离”。越小越好。采样需要多。
CLIP:文本和图像经过Encoder之后的距离需要符合“对应越近,不对应越远”。
训练Decoder:
- 将大图下采样成小图,训练小图变大图。
- 或者不是小图,输入是潜在表征;训练一个Auto-Encoder。
训练Diffusion:
noise加在中间产物上,同上。
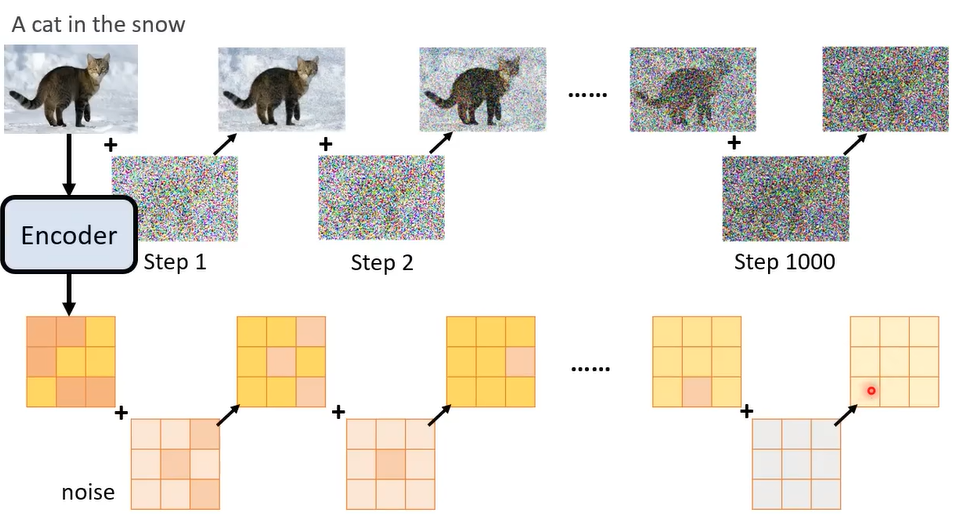
3. 背后的数学原理
3.1 VAE ≈ DDPM
3.2 训练
- 从数据中采样。
- 选取时间步。
- 采样噪声。
- 注意都是从 $x_{0}$ 开始加噪,$x_{0}$ 和 $\epsilon$ 进行加权和,其中 $\alpha$ 随时间步越来越小,就是原图像越小,噪声越大。
- $\epsilon_{\theta}$ 是神经网络,Loss就是噪声的误差,梯度下降,学会预测噪声。
- 直到收敛。
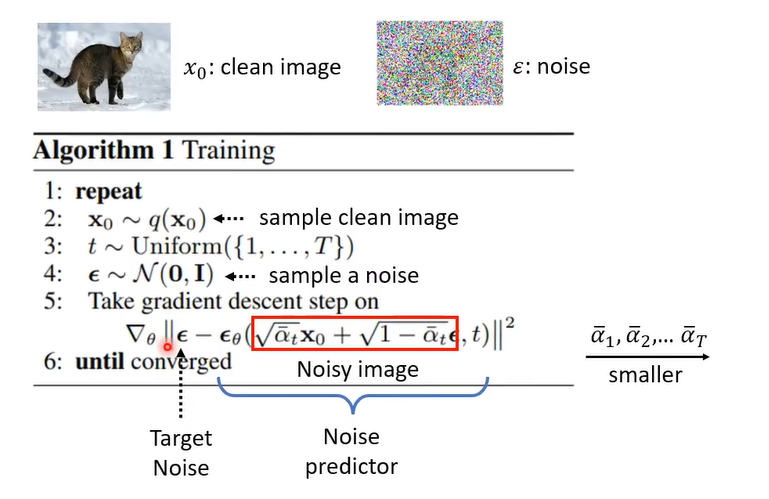
那为什么不是连续加噪,而都是从原始图像上进行一次加噪呢?见之后的数学原理。
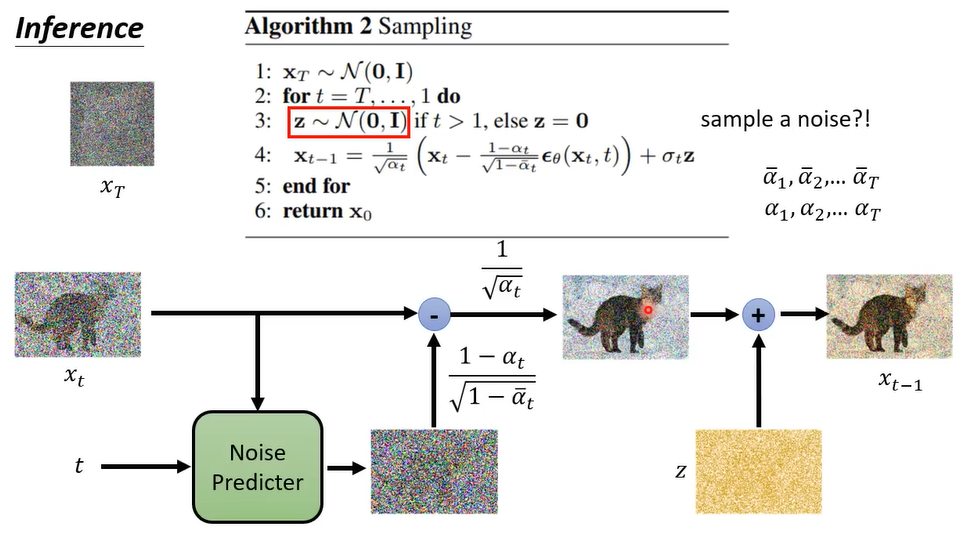
3.3 采样
- 从高斯分布中采样噪声 $x_{T}$。
- 进行T步的循环:
- 每一次都需要再一次从高斯分布中采样噪声 $z$。
- 原始图像减去神经网络预测出来的噪声然后加上噪声 $z$ 。
- 为什么需要另外再产生一个噪声,以及 $\alpha$ 和 $\bar{\alpha}$ 怎么计算出来的?
3.4 数学原理
3.4.1 本质的目标
从一个简单的高斯分布中采样然后经过神经网络得到一个复杂分布中的图片。而这个复杂分布和真实分布越接近越好。
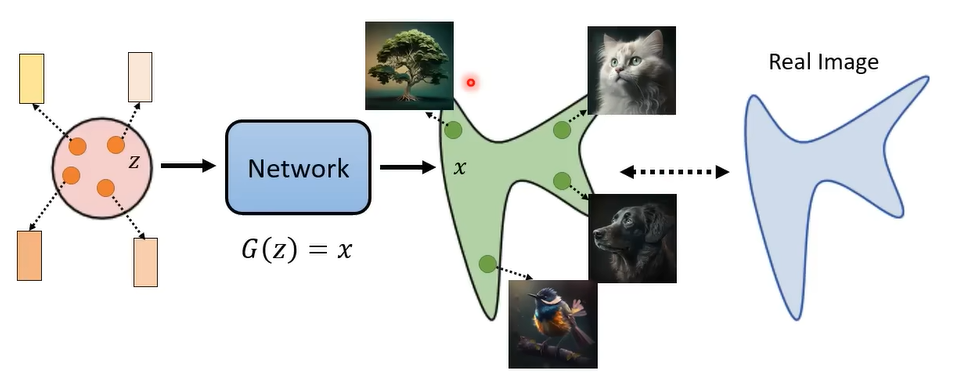
而对于文字生成就是在神经网络中加入条件。
如何衡量两个分布越接近越好这件事? -> 最大似然估计
- 从真实分布中采样数据 $x$ 的概率 $P_{data}(x)$。
- 从神经网络预测出的分布中采样数据 $x$ 的概率 $P_{\theta}(x)$ 。(假设能够计算)
- 最大似然估计,此时的参数是最好的。
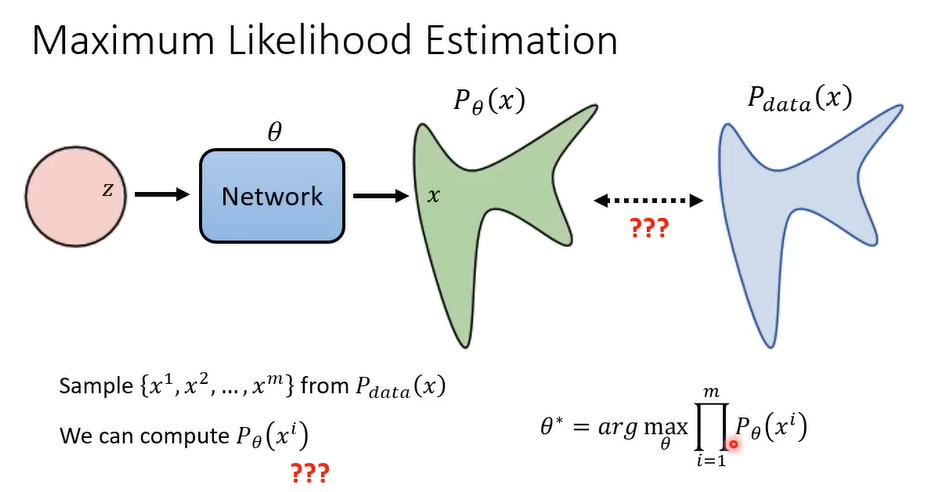
数学推导:
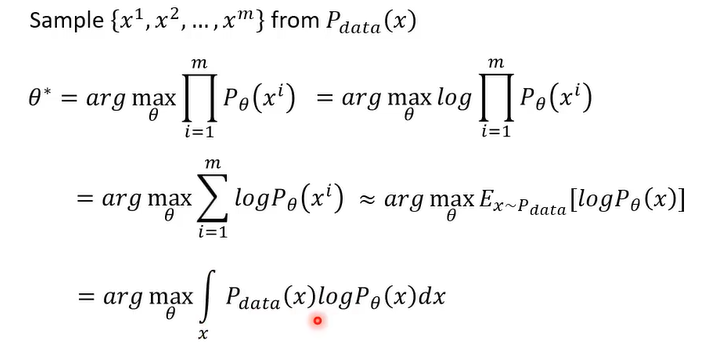
然后加了一项不会对 $\theta$ 有影响的项。好处是合并之后:
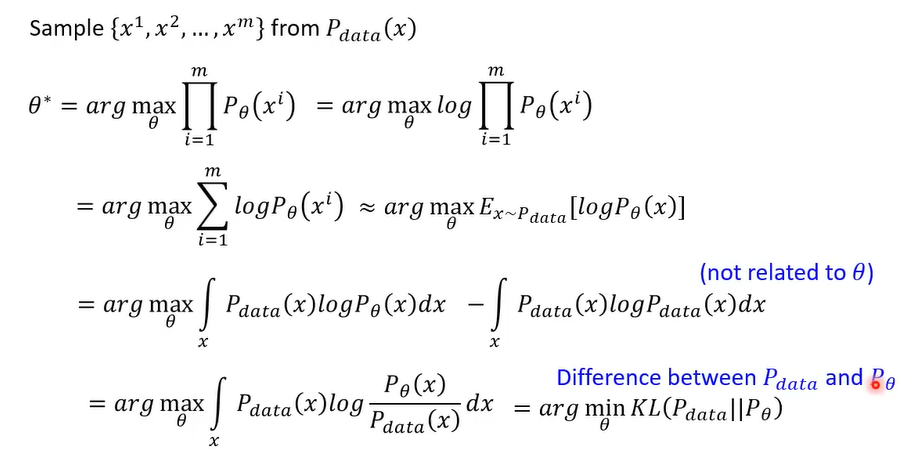
所以最大似然估计就是最小化KL散度。
3.4.2 VAE
要估计 $P_{\theta}(x)$ 可以转化成一个条件概率:
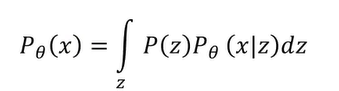
VEA输出的 $G(z)$ 是一个高斯分布的均值。
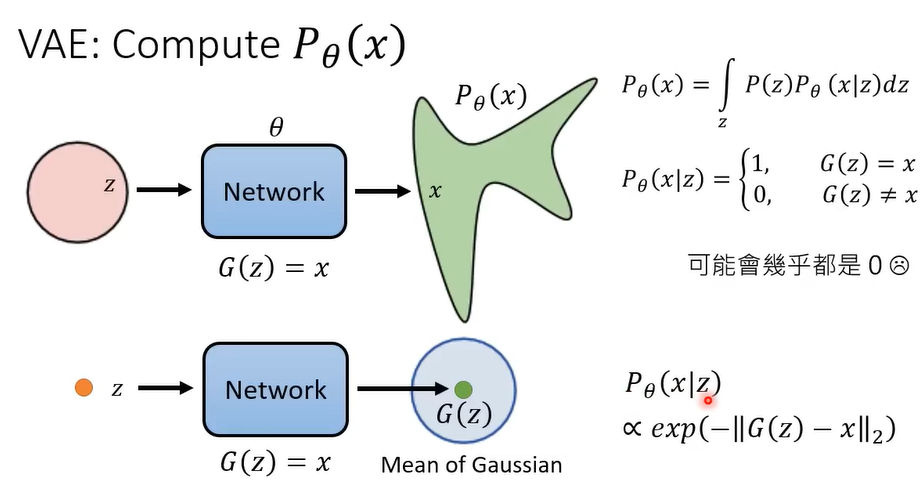
推断下界(Lower Bound):

3.4.3 DDPM
其中为 $-|| G(x_{t})-x_{t-1}||_{2}$ 。